矩阵扩展-算卷积算法介绍及C语言代码实现

1. 矩阵扩展算法——简单的算卷积

接着上文，矩阵进行更深入的学习就需要学习更多的处理了，矩阵被运用在很多的领域，这里简单以计算机图形处理的重要概念——卷积，为例进行说明：

卷积。用一个模板去和另一个图片对比，进行卷积运算。目的是使目标与目标之间的差距变得更大。卷积在数字图像处理中最常见的应用为锐化和边缘提取，
此外，在人工智能中的图像处理也极为常见，这里的运算介绍不提供繁杂的公式（相信短时间内也看不懂）使用Zero padding，unit strides（零填充，单位滑动）的计算方式进行举例。

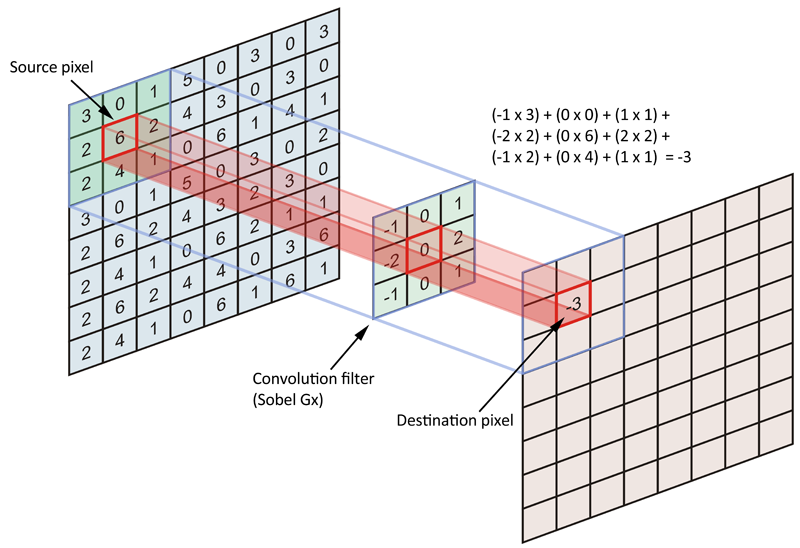
（图片来自外国的学术论坛datascience）

对于此类计算，有两个矩阵a和b，矩阵a是原矩阵，b是卷积核，他们的运算过程是，首先对b矩阵进行倒置，如：

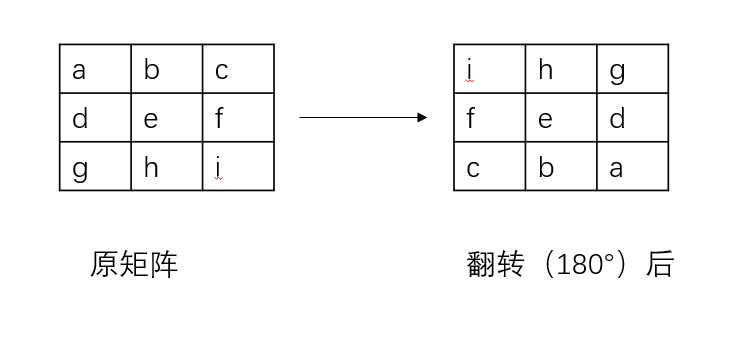
        接着，再将待处理矩阵的部分与卷积核进行逐个进行相对应的运算，本例子由于按照边缘’零’处理的方式，因此边缘全部按照0进行运算，如图运算的过程为：0*1+0*2+0*3+0*2+1*1+2*2+0*1+1*2+2*1=9，这样的一个值计算完成后，对每一个值再度进行运算即可。

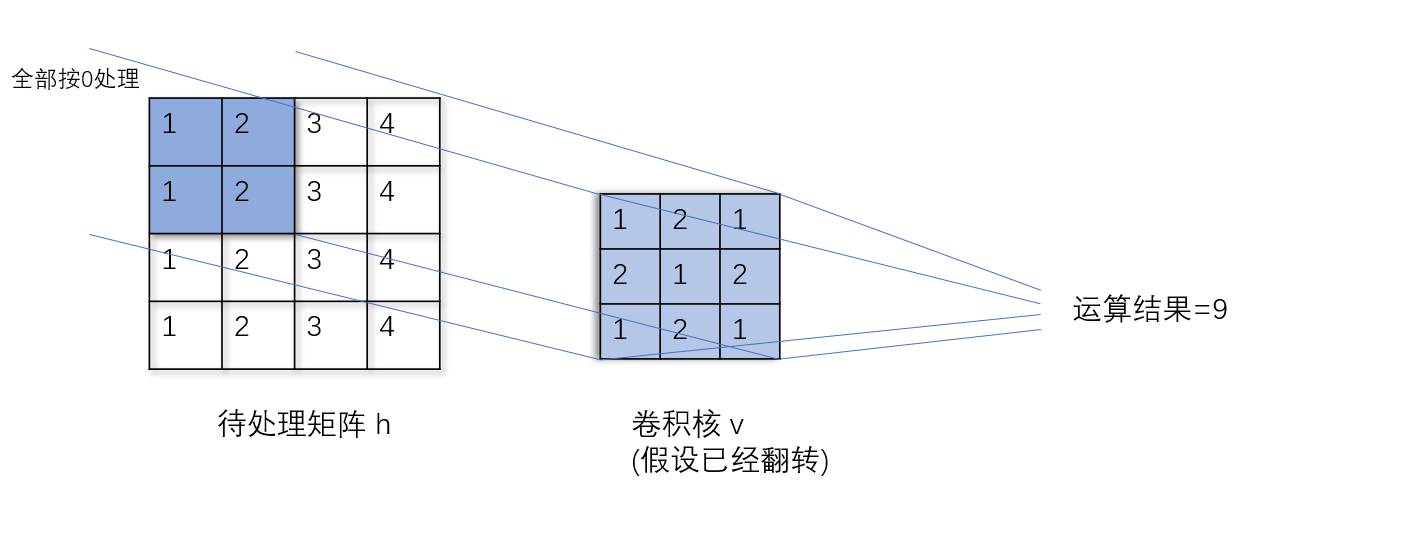
以卷积核为3*3为例，代码样例为：

#include <iostream>
using namespace std;
const int maxn = 105;
int n,m;
int org[maxn][maxn]={0};
int ker[3][3]={0};
int ans[maxn][maxn]={0};
int main(){
    cin>>n>>m;
 
    //待处理的矩阵
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>org[i][j];
        }
    }
    //直接以倒置的方式进行输入
    for(int i=2;i>=0;i--){
        cin>>ker[i][2]>>ker[i][1]>>ker[i][0];
    }
    //卷积运算    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            int tmp=0;
            for(int a=0;a<3;a++){
                for(int b=0;b<3;b++){
                    tmp += (ker[a][b] * org[i-1+a][j-1+b]);
                }
            }
            ans[i][j]=tmp;
        }
    }
 
    //结果输出
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cout<<ans[i][j]<<' ';
        }
        cout<<endl;
    }
    
    return 0;
}